University of California, San Diego
Physics 1b - Thermal Physics & Electromagnetism

H. E. Smith   Spring 2000

Physics 1B - Tutorial #7


I. Complete Circuits

  • A. Light a bulb using a single battery and a single wire. Observe and record the behavior (i.e., brightness) of the bulb when objects made out of various materials are inserted into the circuit. (Try materials such as paper, coins, pencil lead, eraser, your finger etc.)

  • B. Carefully examine a bulb. Two wires extend from the filament of the bulb into the base. You probably cannot see into the base, however, you should be able to make a good guess as to where the wires are attached. Describe where the wires attach.
    One wire attaches to the contact at the center of the base - note that it is surrounded by insulation. The other wire attaches to the metallic side of the bulb base.

    On the basis of the observations that we have made, we will make the following assumptions:

    1. A flow of charge exists in a complete circuit from one terminal of the battery, through the rest of the circuit, back to the other terminal of the battery, through the battery and back around the circuit. We call this flow electric current. (Of course, what you are seeing is the luminous power output of the bulb, which is related to the power consumed and to the current by P = VI = I2R. We must be a little careful about quantitative comparisons of the brightnesses of lightbulbs because the response of the human eye is logarithmic rather than linear.).
    2. For identical bulbs, the bulb brightness can be used as an indicator of the amount of current through that bulb: the brighter the bulb, the greater the current.

    • Starting with these assumptions, we will develop a model that we can use to account for the behaviour of simple circuits.

    II. Bulbs in Series

    Set up a two-bulb circuit with identical bulbs connected one after the other as shown. Bulbs connected in this way are said to be connected in series.
  • A. Compare the brightness of the two bulbs with each other. (Pay attention only to large differences in brightness. You may notice minor differences if two "identical" bulbs are, in fact, not quite identical.) Use the assumptions that we have made in developing our model for electric current to answer the following questions.
    1. Is current "used up" in the first bulb, or is the current the same through both bulbs?
      It is the same through both.

    2. Do you think that switching the order of the bulbs might make a difference? Check your answer.
      No, switching doesn't make any difference

    3. On the basis of your observations alone, can you tell the direction of the flow through the circuit?
      No, looking at the bulbs won't enlighten you as to which way the current flows. If you look at the battery, however, you can see the positive (+) and negative (-) terminals marked; this should tell you which way the current flows.

    • Two bulbs in series

  • B. Compare the brightness of each of the bulbs in the two-bulb circuit with that of a bulb in a single-bulb circuit. Use the assumptions that we have made in developing our model for electric current to answer the following questions.
    1. How does the current through the bulb in a single-bulb circuit compare with the current through the same bulb when it is connected in series with a second bulb? Explain.
      The bulbs are much dimmer in the two bulb circuit. You have doubled the resistance and halved the current

    2. What does your answer to question 1 imply about how current through the battery in a single-bulb circuit compares to the current through the battery in a two-bulb series circuit? Explain.
      If the current through the bulbs is halved, the current through the battery is also halved.

  • C. We may think of a bulb as presenting an impediment, or resistance, to the current in the circuit.
    1. Thinking of the bulb in this way, would adding more bulbs in series cause the total impediment to the flow, or total resistance, to increase, decrease, or stay the same as before?
      Adding more bulbs (resistors) in series increases the resistance.

    2. Formulate a rule for predicting how the current through the battery would change (i.e., whether it would increase, decrease, or remain the same) if the number of bulbs connected in series were increased or decreased.
      If the resistance of 1 bulb is R then the total resistance of n bulbs in series is nR.

    III. Batteries in Series

    Using the 2 bulbs in series add an extra battery in series with the first so that their voltages both act in the same direction. Draw the circuit you have created.

  • A. Compare the brightness of the 2 light bulbs with 2 batteries in series to their brightness with one battery only. Should the brightness of each bulb in your 2 battery/2 bulb circuit be the same as in the 1 battery/1 bulb circuit?
    You have doubled the voltage and doubled the resistance; the current/brightness of each bulb in the 2 battery/2 bulb circuit should be the same as in the 1 battery/1 bulb circuit.

  • B. Briefly connect the 2 batteries to a single light bulb. (Just touch the terminal). What do you see?
     With two batteries you have doubled the current and the voltage through a single bulb, resulting in power (P = VI = I2R) 4X larger.

  • C. Turn one of the batteries around. What happens?
     If the batteries have the same voltage the net potential difference across the two batteries is zero; there will be no current.

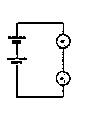
    • Batteries in series

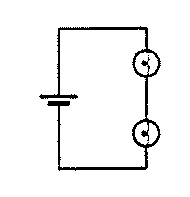
    IV. Bulbs and Batteries in Parallel

    Set up a two-bulb circuit with identical bulbs so that their terminals are connected together as shown. Bulbs connected together in this way are said to be connected in parallel.

  • A. Compare the brightness of the bulbs in this circuit.
    1. What can you conclude from your observation about the amount of current through each bulb?
       The bulbs have the same brightness, thus carry the same current.

    2. Describe the current in the entire circuit. Base your answer on your observations. In particular, how does the current through the battery seem to divide and recombine at the junctions of the two parallel branches?
       The current through the battery must be the sum of the currents through the bulbs.

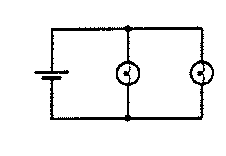
    • Two bulbs in parallel

  • B. Is the brightness of each bulb in the two-bulb parallel circuit greater than, less than, or equal to that of a bulb in a single-bulb circuit? Disconnect one bulb and check your answer.
     The brightness (current, power) is the same.
    1. How does the amount of current through a battery connected to a single bulb compare to the current through a battery connected to a two-bulb parallel circuit? Explain, based on your observations.
      The current through the two-bulb parallel circuit is twice the current through a single bulb circuit.

  • C. Formulate a rule for predicting how the current through the battery would change (i.e., whether it would increase, decrease, or remain the same) if the number of bulbs connected in parallel were increased or decreased. Base your answer on your observations of the behavior of the two-bulb parallel circuit and the model for current.
    The current through the battery increases as the number of bulbs connected in parallel: n bulbs in parallel produces current nI compared with a single bulb.

    What can you infer about the total resistance of a circuit as the number of parallel branches is increased or decreased?
     Resistance for n parallel resistances will be R/n.

  • D. With both bulbs connected in parallel add a second battery in parallel. Does this affect the brightness of the bulbs?
    No, or hardly at all.

    If the 2 batteries had slightly different voltages (maybe one is a little flat) would you expect the bulbs to change a little in brightness as the second battery is added?
     If the second battery has a larger voltage, both bulbs will have this larger p.d. across their terminals, thus higher current and will be brighter.

  • E. How would you compare the current through each battery with the current through a single battery?
    Each battery in parallel will have half the current of a single battery.

    Would the 2 batteries in parallel be able to light the bulbs for a longer period of time than a single battery?
     Yep, twice as long.

    V. More Complicated Circuits

  • A. The circuit at right contains three identical bulbs and a battery. You may use 2 batteries in series to make a higher voltage. Connect and disconnect a wire to act as a switch.
    1. Predict the relative brightness of the bulbs in the circuit with the switch closed. Explain.
      Swith closed is equivalent to B & C in parallel with the combined resistance RBC in series with A. RA = 1R; RBC = R/2. Total resistance = 1.5R. All current will flow through A, then split between B and C. B and C will have half the current and one-quarter (P=I2R) the power of A.

    2. Predict how the brightness of bulb A changes when the switch is opened. Explain.
      With the switch closed no current will flow through C. All current goes through A & B. Total resistance = 2R, so this circuit has smaller total current than above (by 1.5/2.0 = 3/4). A and B will be fainter than A above, brighter than B or C.
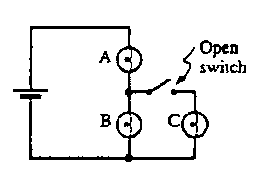
  • B. Predict the relative brightness of bulbs B1, B2, and B3 in the circuits shown below. (A dashed box has been drawn around the network of circuit elements that is in series with each of these bulbs.)
    1. What does your prediction imply about the relative current through the batteries? Explain.
      • In Circuit 1 total resistance R = 2R; current through B1 is I1 = V/2R..
      • In Circuit 2 total resistance R = 1.5R; current through B2 is I2 = V/1.5.
      • In Circuit 3 total resistance R = 3R; current through B1 is I1 = V/3R.
      B2 will be brightest, followed by B1, then B3.

    2. Put together the circuits so that you can check your answers. Resolve any conflicts between your answers and your observations.
    		•  
     
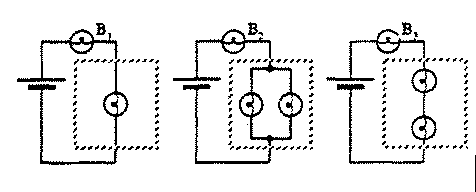
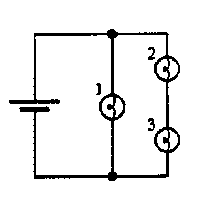
  • C. Before setting up the circuit shown at right:
    1. Predict the ranking of the currents through the battery and each bulb (iBat, i1, i2, and i3). Explain.
      In this case R1 = R and R23 = 2R. Bulb 1 will have twice the current of Bulbs 2 and 3 (which must have the same current). The current through the battery will equal the sum of the currents through Bulb 1 and Bulbs 2,3.
      • i1 = 2 i2
      • i1 = 2 i3
      • iBat = 1.5 i1 = 3 i2.

    Set up the circuit and check your predictions. If your observations and measurements are not consistent with your predictions, resolve the inconsistencies.



    • Physics 1B Home       Tutorials   Tutorial #6   Tutorial #8  

    Gene Smith

    Last modified: Thurs., 18 May 2000