| H. E. Smith | Spring 2000 |

| Physics 1B - Tutorial #5 |


potential difference = (PEtop - PEbottom)/m = gh = 9.8 m/s2 x 1450m = 14,210 J/kg
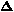 (PE/m)/
(PE/m)/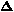 l = gh/h = g
l = gh/h = g
(n.b. Here the potential gradient is just the gravitational
field, just as the gradient of the electric potential is the electric
field)
potential gradient =
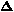 (PE/m)/
(PE/m)/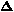 l = g 1450m/1600m = 0.9g
l = g 1450m/1600m = 0.9g
The effective gravitational field is less.
Elevation contours.
No, and Jennie didn't die at 20,000V. Although the potential of the wire and
the bird is high with respect to the ground, the potential difference
across the bird is negligible and does no harm. Similarly, it does no harm to
raise someone to 30,000 ft. - high gravitational potential. The only harm
comes when someone at high potential is connected via a steep path to a region
of low potential -
The field is strongest where the contours are closest together - up "1",
and weakest where the contours are furthest apart - up "2"
E =
A second plate, charged with -1 C/m is placed 1cm below the positively charged
plate, parallel to it.
E = 0 above upper/below lower plate
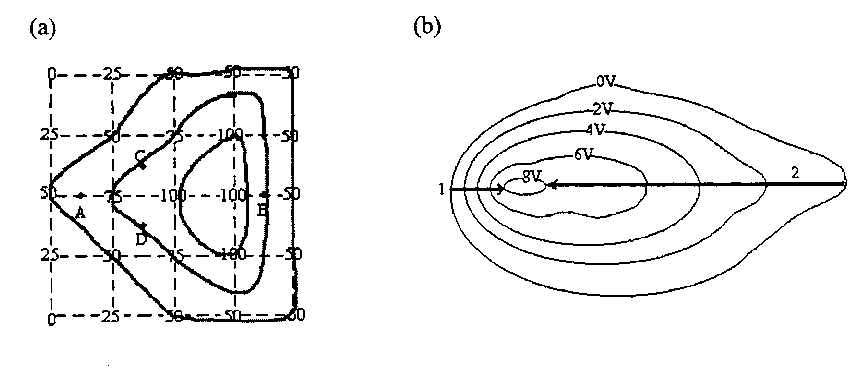
B. E = - dV/dl = 50V/1cm = 5000 V/m (toward right)
C. E = - dV/dl = 50V/1.4cm = 3570 V/m (toward upper left)
D. E = - dV/dl = 50V/1.4cm = 3570 V/m (toward lower left)
 /2
/2 0 = 1 C/m2/2 .
8.85 x10-12m2 N-1 C-2
= 5.65 x 1010N/C (away from plate)
0 = 1 C/m2/2 .
8.85 x10-12m2 N-1 C-2
= 5.65 x 1010N/C (away from plate)

![]() Physics 1B Home
Physics 1B Home
![]() Tutorials
Tutorials
![]() Tutorial #4
Tutorial #4
![]() Tutorial #6
Tutorial #6