University of California, San Diego
Physics 1b - Thermodynamics, Electricity & Magnetism

 |
Physics 1B - Tutorial #1
|

- What temperature has the same numerical value in Celsius (Centigrade)
and Fahrenheit? Is there a temperature which has the same value on the
Celsius and Kelvin (thermodynamic) scales?
TC = TF at -40°
A circular iron plate has a coefficient of linear expansion of
10-5K-1. At 20°C it has a central circular hole of
radius 2 inches. The plate is then heated to 40°C.
- Does the size of the hole increase, decrease or remain the same?
The radius of the hole increases.
Calculate the numerical value of the radius at 40C.
r = 2.0004 inches.
The surface area of the earth is approximately
5 x 1014m2. The scale height (thickness) of the
earth's atmosphere is 104m. A cubic meter of air at room
temperature and a pressure, P = 1 atmosphere, has a mass of 1.3kg.
- Estimate the mass of air on the earth.
Volume of air = (5 x 1014m2) x (104m) =
5 x 1018m3. Mass of air =
(5 x 1018m3) x (1.3 kg/m3) =
6.5 x 1018kg.
A mole of air has a mass of 0.029kg (Why?). How many molecules
does the earth's atmosphere contain?
Air is 80% N2 and 20% O2 so the mass of 1 mole
is between 28 and 32 grams (0.8 x 28g + 0.2 x 32g). Number of moles
= 2.2 x 1020 moles. Number of molecules =
(2.2 x 1020) x (6 x 1023) = 1.3 x 1044
molecules.
Assuming that the atmosphere has become completely mixed over the
last 2000 years, how many molecules from Julius Ceasar's last breath
are in your lungs at the current moment.
Estimate the volume of the lungs as two cylinders 30cm in length, 5cm in
radius.
V = 2 lungs x 3(~pi) x (0.05m)2 x 0.3m = 0.005 m3.
Julius Caesar's last gasp had
(1.3x1044)x(0.005 m3)/(5x1018m3)
= 1023 molecules,
of which
(1023)x(0.005 m3)/(5x1018m3)
(about 100) are in your lungs right now.
You use superglue to attach a strip of copper to a strip of
aluminum at 20C. Coefficients of linear expansion:
Cu = 16.6 x 10-6K-1;
Al = 25 x 10-6K-1.
- What will happen if you heat the strips to 40C? Make a sketch.
The strips will bend into an arc of circle; the more expansive material will
be on the outer circumference of the arc.
What will happen if you cool the strips to 0C? Make a sketch.
The strips will bend into an arc in the opposite direction.
How will the behaviour of the strips depend upon thickness: i.e.
if they are very thick (like metal bars) or very thin (like paper strips).
Thin strips will bend more than thick bars.
Can you think of practical uses of devices employing this behaviour?
Thermostats, of course; any mechanism in which you want to regulate
temperature or turn a device on or off if it gets too hot or too cold.
For a device made of two metal strips such as this one, what parameters
are important in determining how the strips bend? Which would make bending
larger? Which would make bending smaller? (Consider the coefficients of
linear expansion, initial & final temperatures, strip length &
thickness, anything else that you think might be important.)
- Strip length: longer strips will bend more.
- Temperature difference from "normal": greater T difference, greater
bending.
- Difference in coefficients of expansion between materials; the
greater the difference in coefficients, the greater the bending.
(OPTIONAL) Suggest a formula to describe the bending using the
parameters discussed above in (e).
Let the strip consist of two metals, with expansion coefficients
 1 and
1 and
 2, each with
thickness t/2 and original
length, l0. Suppose that metal #1 expands more (or contracts less)
than metal #2 so that, at temperature T = T0 +
2, each with
thickness t/2 and original
length, l0. Suppose that metal #1 expands more (or contracts less)
than metal #2 so that, at temperature T = T0 +
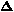 T, the length of metal #1 is
l1 = R
T, the length of metal #1 is
l1 = R , where R is the
(unknown) radius of the arc formed by the bimetallic strip and
, where R is the
(unknown) radius of the arc formed by the bimetallic strip and
 is the angle subtended by the arc.
Metal #2 has length l2 =
(R + t/2)
is the angle subtended by the arc.
Metal #2 has length l2 =
(R + t/2) . The difference in
these lengths is (t/2)
. The difference in
these lengths is (t/2) which must
equal (
which must
equal ( 2 -
2 -
 1)
1)
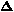 T l0. Solving for
T l0. Solving for
 =
2(
=
2( 2 -
2 -
 1)
1)
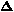 T l0/t.
T l0/t.
As you learned in Physics 1A, rocket propulsion employs the principle
of Conservation of Linear Momentum. Ideally, the burning (oxidation)
of hydrocarbon fuels produces water (H2O) and carbon dioxide
(CO2) which are expelled at high velocity. Sketch a diagram of
how the burning of rocket fuel propels a rocket forward.
- A rocket of mass 1 metric ton (1000 kg) expels
CO2 with an exhaust speed of 1000m/s.
How much CO2 must be ejected to accelerate the rocket by
1000 m/s.
Let mr be the initial mass of the rocket including all its fuel and
mf be the mass of fuel expended. In the initial reference frame of
the rocket, mfvf =
(mr-mf)vr. In this case
vf(backward) = vr(forward) and mf =
mr/2 = 500kg. (Note that the expended fuel is accelerating both
the rocket and the unexpended fuel - the most effective way to accelerate the
rocket is to expel the fuel at the highest possible velocity, hence at the
highest possible temperature.)
Compare the rms speeds of water and carbon dioxide at a temperature of
1000 K.
m(H2 O) = 18 g/mole; m(CO2) = 76 g/mole. The speed of
(lighter) water molecules will always be a factor of sqrt(76/18) = 2.06 higher
than carbon dioxide. At 1000K water molecules will have
vrms = 1175 m/s and corbon dioxide,
vrms = 570 m/s.
Does the rms speed depend upon the pressure?
Nope; then what role does the pressure in the balloon play in propelling
it forward in the next question?
Use a balloon to demonstrate rocket propulsion. What is the typical
speed of the escaping molecules? Do they carry away momentum?
The molecules escaping from the balloon are moving at speeds typical of room
temperature, vrms = 500 m/s. Remember that momentum is a
vector; the escaping molecules carry away (negative) momentum leaving the
balloon with a net positive momentum.
The next time you are home, take apart your thermostat and demonstrate to
your parents how a bi-metallic strip works. Four brownie points if you
can reassemble the thermostat and your home heating system still works,

 Physics 1B Home
Physics 1B Home
 Tutorials
Tutorials
 Tutorial #2
Tutorial #2
Gene Smith
Last
modified: Tues., 4 April 2000


 1 and
1 and
 2, each with
thickness t/2 and original
length, l0. Suppose that metal #1 expands more (or contracts less)
than metal #2 so that, at temperature T = T0 +
2, each with
thickness t/2 and original
length, l0. Suppose that metal #1 expands more (or contracts less)
than metal #2 so that, at temperature T = T0 +
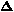 T, the length of metal #1 is
l1 = R
T, the length of metal #1 is
l1 = R , where R is the
(unknown) radius of the arc formed by the bimetallic strip and
, where R is the
(unknown) radius of the arc formed by the bimetallic strip and
 is the angle subtended by the arc.
Metal #2 has length l2 =
(R + t/2)
is the angle subtended by the arc.
Metal #2 has length l2 =
(R + t/2) . The difference in
these lengths is (t/2)
. The difference in
these lengths is (t/2) which must
equal (
which must
equal ( 2 -
2 -
 1)
1)
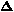 T l0. Solving for
T l0. Solving for
 =
2(
=
2( 2 -
2 -
 1)
1)
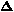 T l0/t.
T l0/t.

![]() Physics 1B Home
Physics 1B Home
![]() Tutorials
Tutorials
![]() Tutorial #2
Tutorial #2