The conducting loop shown above has area A = 1m2
(1m on a side) and is moving with v=1m/s into a magnetic field
B = 10-4T. Graph the current in the loop as a function
of time.
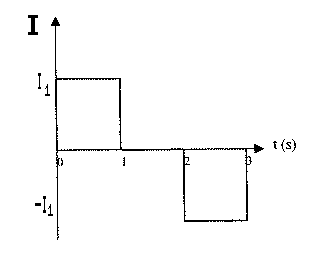 |
From Faraday's Law
 =
-d =
-d /dt = B . dA/dt = Blv
= 10-4T.1m.1m/s = 10-4V /dt = B . dA/dt = Blv
= 10-4T.1m.1m/s = 10-4V
as the loop enters the field. If emf and current are positive
counter-clockwise, the current will behave as shown on the left, with
I1 = 10-4A. |
An apartment complex is supplied by single-phase AC from a power plant
5-km away. The wire that runs from the power plant to the complex and back
has a resistance per unit length of 1 x 10-5
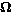 /m, supplying 100,000W.
/m, supplying 100,000W.
- Calculate the resistive power losses in the wire if the AC is supplied
at 110V.
The total wire resistance is 1 x 10-5 . (5000m + 5000m)
= 0.1 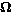 . The power supplied is
P = VI so that I = 100,000W/110V = 910A. The power lost to heating the wire
due to its resistance is P = I2R = (910A)2.
0.1
. The power supplied is
P = VI so that I = 100,000W/110V = 910A. The power lost to heating the wire
due to its resistance is P = I2R = (910A)2.
0.1 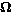 = 83kW. In other words, the power
plant has to produce 183kW in order to deliver 100kW, losing 45% to
resistive heating.
= 83kW. In other words, the power
plant has to produce 183kW in order to deliver 100kW, losing 45% to
resistive heating.
Calculate the resistive power losses in the wire if the AC is supplied
at 500kV (typical of US electric distribution).
In this case the current is much lower, I = 100,000W/500,000V = 0.2A
and the resistive losses, P = (0.2A)2.
0.1 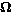 = 0.004W, are negligible.
= 0.004W, are negligible.
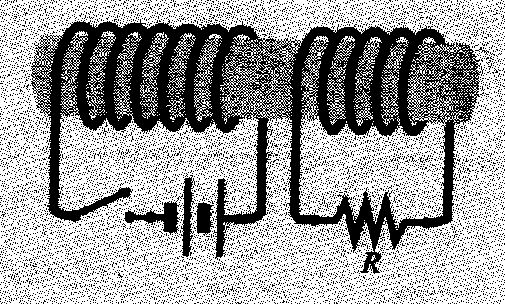
Design a way to transform AC provided at 500kV to 110V.
You need a transformer, one of those big cylinders that you see
mounted on power poles which uses magnetic induction such that
Vsource/Vhousehold = Ns/Nh,
where N is the number of turns of wire on the appropriate side of the
transformer. In this case, Vsource/Vhousehold =
500,000V/110V = 4545, so the turn ratio of this step-down
transformer is Ns/Nh = 4545 (e.g.
if the output - 110V - side of the transformer has 100 turns, the input
side would need 454,545 turns).

 Physics 1B Home
Physics 1B Home
 Tutorials
Tutorials
Gene Smith
Last
modified: Tues., 6 June 2000



 =
-d
=
-d /dt = B . dA/dt = Blv
= 10-4T.1m.1m/s = 10-4V
/dt = B . dA/dt = Blv
= 10-4T.1m.1m/s = 10-4V 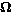 /m, supplying 100,000W.
/m, supplying 100,000W.
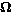 . The power supplied is
P = VI so that I = 100,000W/110V = 910A. The power lost to heating the wire
due to its resistance is P = I2R = (910A)2.
0.1
. The power supplied is
P = VI so that I = 100,000W/110V = 910A. The power lost to heating the wire
due to its resistance is P = I2R = (910A)2.
0.1 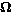 = 83kW. In other words, the power
plant has to produce 183kW in order to deliver 100kW, losing 45% to
resistive heating.
= 83kW. In other words, the power
plant has to produce 183kW in order to deliver 100kW, losing 45% to
resistive heating.
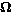 = 0.004W, are negligible.
= 0.004W, are negligible.